Last week there was a brief but interesting conversation on Twitter about the practice of “co-first” authors on scientific papers that led me to do some research on the relationship between author order and gender using data from the NIH’s Public Access Policy.
I want to note at the outset that this is my first foray into analyzing this kind of data, so I would love feedback on the data, analyses and finding, especially links to other work on the subject, as I know some of these issues have been addressed elsewhere.
A long post follows, but here are some main things I found:
- The number of female authors falls off as you go down the list of authors of a paper, with fewer than 30% of senior authors female.
- Contrary to my expectation, there doesn’t seem to be a bias to put the male author first when there are male-female co-first author pairs.
- There are, however, far fewer male-female co-first author pairs than there should be based on the number of male and female first and second authors.
- The same thing holds true more generally for first-second author pairs. There is a deficit of cross gender pairs and a surplus of same gender pairs.
- Part (and maybe most) of this effect is due to an overall skew in gender composition of authors on papers.
- If you are female, there is a 45% chance that a random co-author on one of your papers is female. If you a male, there is only a 35% chance that a random co-author on one of your papers is female.
Before I explain how I got all this, let me start with a quick explainer about how to parse the list of authors on a scientific paper.
By convention in many scientific disciplines (including biology, which this post is about), the first position on the author list of a paper goes to the person who was most responsible for doing the work it describes (typically a graduate student or postdoc) and the last position to the person who supervised the project (typically the person in whose lab the work was done). If there are more than two authors an effort is made to order them in rough relationship to their contributions from the front, and degree of supervision from the back.
Of course a single linear ordering can not do justice to the complexity of contribution to a scientific work, especially in an era of increasingly collaborative research. One can imagine many better systems. But, unfortunately, author order is currently the only way that the relative contributions of different people to a work is formally recorded. And when a scientist’s CV is being scrutinized for jobs, grants, promotions, etc… where they are in the author order matters A LOT – you only really get full credit if you are first or last.
Because of the disproportionate weight placed on the ends of the author list, these positions are particularly coveted, and discussions within and between labs about who should go where, while sometimes amicable, are often difficult and contentious.
In recent years it has become increasingly common for scientists to try and acknowledge ambiguity and resolve conflicts in author order by declaring that two or more authors should be treated as “co-first authors” who contributed equally to the work, marking them all with a * to designate this special status.
But, as the discussion on Twitter pointed out, this is a bit of a ruse. First is still first, even if it’s first among equals (the most obvious manifestation of this is that people consider it to be dishonest to list yourself first on the author list on your CV if you were second with a * on the original paper).
Anyway, during this discussion I began to wonder about how the various power dynamics at play in academia played out in the ordering of co-equal authors. And it seemed like an interesting opportunity to actually see these power dynamics at play since the * designation indicates that the contributions of the *’d authors was similar and therefore any non-randomness in the ordering of *’d authors with respect to gender, race, nationality or other factors likely reflects biases or power asymmetries.
I’m interested in all of these questions, but the one that seemed most accessible was to look at the role of gender. There are probably many ways to do this, but I decided to use data from PubMed Central (PMC), the NIH’s archive of full-text scientific papers. Papers in PMC are available in a fairly robust XML format that has several advantages over other publicly available databases: 1) full names of authors are generally provided, making it possible to infer many of their genders with a reasonable degree of accuracy, and 2) co-first authorship is listed in the file in a structured manner.
I downloaded two sets of papers from PMC: 1,355,350 papers in their “open access” (OA) subset that contains papers from publishers like PLOS that allow the free text to be redistributed and reused 424,063 papers from the “author manuscript” (AM) subset that contains papers submitted as part of the NIH’s Public Access Policy. There papers are all available here.
I then wrote some custom Python scripts to parse the XML, extracting from each paper the author order, the authors’ given names and whether or not they were listed as “co-first” or “equal” authors (this turned out to be a bit trickier than it should have been, since the encoding of this information is not consistent). I will comment up the code and post it here ASAP.
I looked at several options for inferring an author’s gender from their given name, recognizing that this is a non-trivial challenge, with many potential pitfalls. I found that a program called genderReader, recommended by Philip Cohen, worked very well. It’s a bit out of date, but names don’t change that quickly, so I decided to use it for my analyses.
I parsed all the files (a bit of a slow process even on a fast computer) and started to look at the data. I’m going to focus on the AM subset here first, because these are all NIH funded papers and thus mostly from the US, so intercountry differences in authorship practices won’t confound the analyses, and because the set is likely more representative of the universe of papers as a whole than is the OA subset. I will try to note where these two datasets agree and disagree.
Of the 424,063 papers in AM, there are 2,568,858 total authors with a maximum of 496 and a wide distribution.
There are 219,559 unique given names (including first name + middle initials), of which about 75% were classified successfully by genderReader as male, mostly male, female, mostly female or unisex. About 25% were not in their database. For the purpose of these analyses, I treated mostly male as male and mostly female as female. I’m sure there’s some errors in this process, but I looked over a reasonable subset of the calls and the only clear bias I saw was that it didn’t do a good job of classifying Asian names – treating most of them as unisex, and thereby excluding them from my analysis. All together there were 1,206,616 male authors, 737,424 female authors and 624,818 who weren’t classified. Of the authors who were classified, 62% were male.
Of the 424K paper 32,304 contained co-equal authors, and 28,184 contained two or more co-first authors (assessed by asking if the co-equal authors were at the beginning of the author list). Of these, 85% (24,087) had exactly two co-first authors and 12% (3,285) had three co-first authors (one had 20 co-first authors, which I’m just going to leave here for discussion). I decided to use only those with exactly two co-first authors for the next set of analyses.
There were a total of 11,340 papers with exactly two co-first authors both of whose genders were inferred. Of these, the author order counts were as follows:
| Count | Percent | ||
|---|---|---|---|
| Male-Male | 4286 | 37.8 | |
| Male-Female | 2479 | 21.9 | |
| Female-Male | 2399 | 21.1 | |
| Female-Female | 2176 | 19.2 |
I will admit I expected to see a lot more papers with Male-Female than Female-Male orders amongst two co-first authors. That is, however, not what the data show.
However, that doesn’t mean there’s not something interesting going on with gender here. First, there’s obviously a lot more male authors than female authors. In this set of papers, only 40.3% of authors in position 1 and 41.0% in position 2 are female. Given this you can easily calculate the expected number of MM, MF, FM and FF pairs there should be.
| Expected | Observed | |
|---|---|---|
| Male-Male | 3994 | 4286 |
| Male-Female | 2776 | 2479 |
| Female-Male | 2696 | 2399 |
| Female-Female | 1874 | 2176 |
Although there doesn’t seem to be a bias in favor of M-F over F-M, there are significantly (p << .0000000001 by Chi-square) fewer mixed gender co-first author pairs than you’d expect given the overall number of male and female co-first authors.
What can explain this? Are young scientists less likely to collaborate across gender lines than within them? Are male and female pairs better able to resolve their authorship disputes, and are thus underrepresented amongst co-first authors? Or are there fewer opportunities for them to collaborate because of biased lab compositions?
First I wanted to ask if there was a similar bias if we looked at all papers, not just the relatively rare co-first author papers. Here is the fraction of female author by position in author list for all papers (excluding the last author for now).
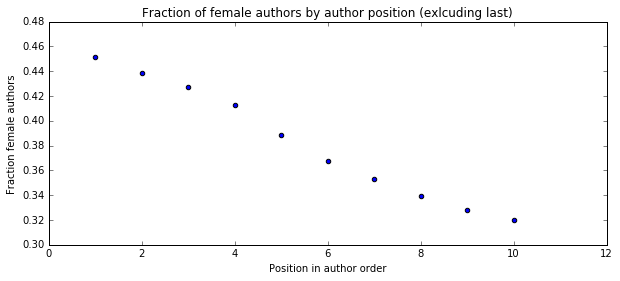
Female authors are most common in the first author position and they are increasingly less represented as you go back in the author order. Maybe this has to do with the well documented problem of academia driving out women between graduate school and faculty position. So next I asked what fraction of senior authors are women.
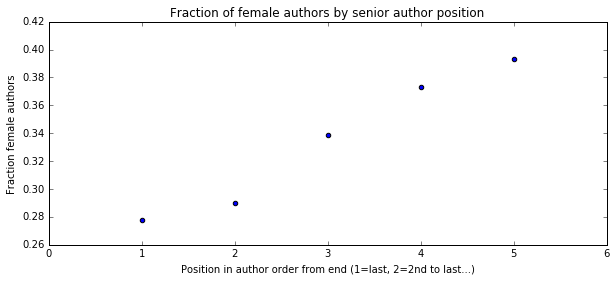
Yikes. Only 28% of senior authors of NIH author manuscripts are female compared to 46% of first authors. That’s horrible.
So what about the question from above. Are mixed gender first and second author pairs less common across all papers, not just co-firsts? The answer is yes.
| Expected | Observed | |
|---|---|---|
| Male-Male | 60052 | 66807 |
| Male-Female | 48874 | 42120 |
| Female-Male | 51623 | 44869 |
| Female-Female | 42014 | 48769 |
Again, there are lots of possible explanations for this, but I was curious about the effect of biased lab composition (if the gender composition of labs is skewed away from parity then you’d expect more same gender author pairs). It’s hard to look at this directly with this data, but if one were going to guess at a covariate for skewed lab gender it would be the gender of the PI, and this I can look at with this data.
So, I next broke the data down by the gender of the senior author.
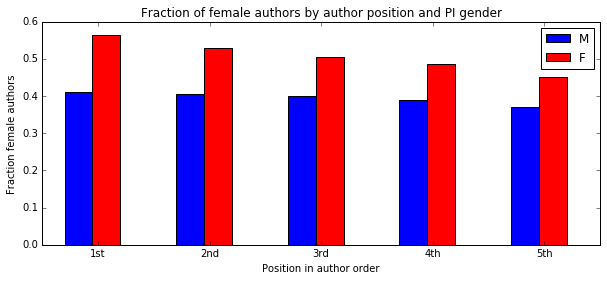
And in tabular form since the data are so striking.
| PI Female | PI Male | |
|---|---|---|
| 1st | 56.3 % | 41.0 % |
| 2nd | 53.0 % | 40.6 % |
| 3rd | 50.6 % | 40.0 % |
| 4th | 48.5 % | 39.0 % |
| 5th | 45.1 % | 37.1 % |
This data very strongly suggests that women are more likely to join labs with female PIs and men more likely to join labs with male PIs. But it doesn’t say why. It could be that people simply choose labs with a PI of their gender, or that PIs select people of the same gender for their labs. This could have to do with direct gender bias, or with lab style or many other things. Or it could be that there’s a hidden field effect here – that different fields have different gender biases, which would drive the gender distribution of labs on average away from parity.
But whatever the reason it’s a clear confounding factor in looking at gender and authorship. Interestingly, the bias against mixed gender first and second authorship is still there (p-values << .0000000001) even if you control for the gender of the PI.
Next I asked if we could detect a skew in the gender composition of the entire author list of papers. So I took sets of papers with number of authors ranging from 2 to 8 (these are the ones for which we have enough data), filtered out papers where one or more authors didn’t have an inferred gender, and compared the distribution of the number of female authors to that expected by the frequency of male and female authors at each position. There is very consistently a skew towards the extremes, with a significant excess in every case of papers with authors of one gender.
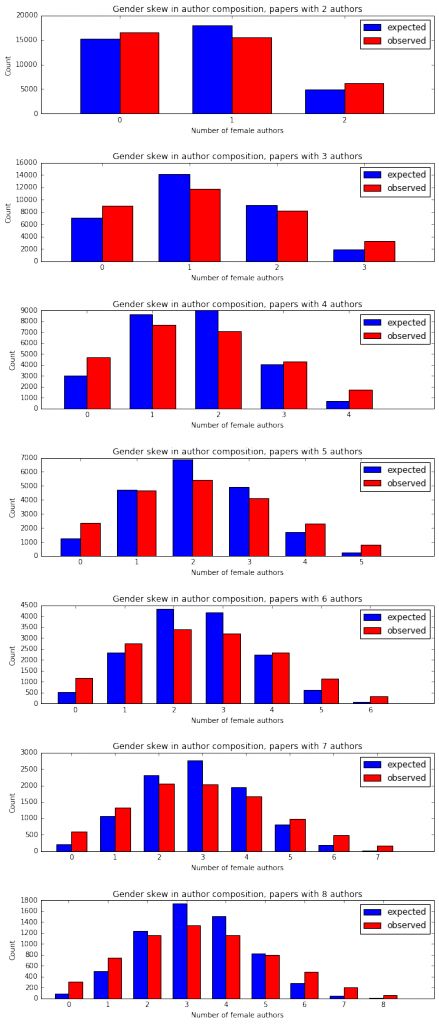
So there’s a pretty systemic skew in the gender composition of authors on papers, but where that skew comes from is unclear. Let’s look at the gender mix of all of the other authors on a paper as a function of the gender of the last author.
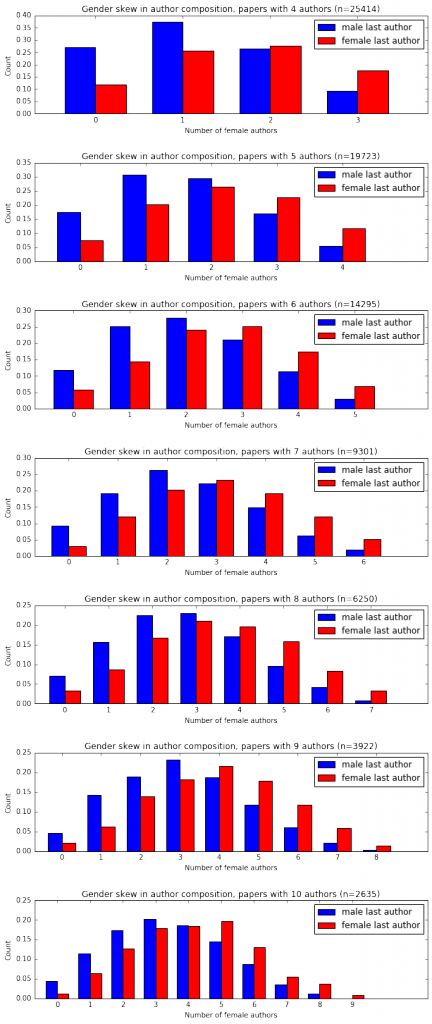
Again, there’s a pretty strong skew. But is this due to the PI’s gender or to a more general gender imbalance? It’s a bit hard to tell from this data alone. It turns out the skew you see after dividing based on the gender of the last author is roughly the same if you divide based on the gender of any other position in the author order. Here, for example, is what you get for papers with six authors.

There’s a lot more one could and should do with this data, and I will come back to it later, but for now I will end with this observation. If you are female, there is a 45% chance that a random co-author on one of your papers is female. If you are male, it goes down to 35%. That’s a pretty big and striking difference, and I’m curious if anyone has a good explanation for it.
13 Comments